УКАЗАНИЯ ЗАОЧНИКАМ

УЧАЩИЕСЯ ОБЯЗАНЫ: регулярно по расписанию посещать учебные занятия школы и своевременно сдавать зачеты.

Учителя на занятиях объясняют учебный материал по программам ве­черних школ, учат решать задачи, примеры, проводят пись­менные работы, дают указания, как самостоятельно работать над усвое­нием материала учебника, а также оказывают помощь отстающим в учебе.

1.ПОМНИТЕ: самостоятельно усвоить школьную программу очень трудно; успешно учится тот, кто не пропускает учебных занятий и выпол­няет все указания и задания учителей.

2.Для прочного усвоения объясненного учителем материала в сво­бодные от занятий дни самостоятельно занимайтесь не менее 2—3 часов.

3.Если Вы поступили в школу с опозданием, приложите максимум усилий, чтобы нагнать упущенное.

4.По предмету надо иметь тетрадь. Записи ведите аккуратно и чисто. Тетрадь поможет Вам при подготовке к экза­менам и сдаче зачетов.

5.Если Вы поехали в командировку или находитесь в отпуске, не пре­рывайте учебу, а в данных условиях найдите время для учебных занятий.

6. Учебный год в заочных классах начинается 1 сентября и

заканчивается 25 мая.

ЧТО НАДО ЗНАТЬ О ЗАЧЕТАХ

Зачет - это проверка знаний учащегося по одному разделу учебного материала. Каждый учащийся должен сдать в течение учебного года 5 зачетов за курс своего класса: Алгебра и начала математического анализа – 3 зачета, Геометрия – 2 зачета.

Перед тем как приступить к подготовке зачетного материала, необхо­димо ознакомиться в учебном плане с разделом изучаемого зачета.

1.По математике, кроме устных зачетов, учащиеся выполняют письменные работы по указа­нию учителей.  Учитель выставляет в зачетном листке учащегося две оценки: за устный ответ и письменную работу. Зачеты оцениваются по пятибалльной системе.

2.Сдача зачетов по срокам является обязательной. Отложить сдачу зачетов можно только по уважительной причине, с разрешения админи­страции школы.

3.Учащиеся переводных классов, не сдавшие всех зачетов к концу учебного года, сдают их с 16 по 30 августа. Заочники, не сдавшие к 1 сен­тября зачеты хотя бы по одному предмету, оставляются на второй год.

4.Зачеты, сданные учащимися, действительны в течение двух лет. (Положение о вечерней школе)

5.К экзаменам допускаются учащиеся, сдавшие все зачеты к 20 мая.

6.Если учащийся не посещает занятий и не сдает зачеты, школа ему напоминает об этом, а затем, если он не приступает к сдаче зачетов, ис­ключает его из состава учащихся.

ЗАЧЕТНЫЕ РАБОТЫ выполняют те, кто не имеет возможности явиться в школу для сдачи зачетов лично: он высылает в адрес заочной школы письменные контрольные работы по каждому зачету. Выполняйте их четко, аккуратно, указывая номер работы, предмет, класс, фамилию, имя, отчество, домашний адрес. Не допускайте списыва­ния с учебника или других пособий: работы, в которых нарушено это требование, не засчитываются.

С ЧЕГО СЛЕДУЕТ НАЧИНАТЬ ИЗУЧЕНИЕ КАЖДОГО ЗАЧЕТА ПО УЧЕБНИКУ

1.     Читая текст параграфа (раздела), прежде всего надо прочитать весь параграф целиком, не задерживая слишком много внимания на трудных местах. При повторном чтении (читать надо медленно, по абзацам, обдумывая каждое слово, каждое предложение) надо продумывать трудные места в учебнике, прочитать к ним разъяснения.

Обращайте внимание на выделенные слова и предложения, они выра­жают главное, что надо хорошо запомнить. Изучив текст, проверьте свои знания вопросам без книги и тетради, на память. Если затрудняетесь дать ответ на какой-либо вопрос, найдите в тексте соответствующий раздел и прочтите его еще раз. Повторять надо до тех пор, пока не будет усвоено все.

2.                      При любой работе с книгой большую пользу приносят конспектирование или запись основных положений, определений. Занимаясь, не спешите делать записи сразу при первом чтении. Читая, отмечайте мысли, факты, цифры, которые Вам покажутся важными. Закончив параграф (главу, раздел), внимательно просмотрите его еще раз и выберите окончательно, что необходимо записать. Изучение материала по математике требует обязательного выполнения упражнений, решения примеров и задач.

3.После того как изучаемый материал усвоен полностью, вы должны

в назначенное время сдать зачет.

Тригонометрические Функции Зачет №1 10 зо

Теория

1.История развития тригонометрии  (презентация)

2. Введение

3. Числовая окружность

4. Числовая окружность на координатной плоскости

5. Синус и косинус,  тангенс и котангенс

6. Тригонометрические функции числового аргумента

7. Тригонометрические функции углового аргумента

2. Введение

Для введения тригонометрических функций понадобится новая математическая модель — числовая окружность.

Для облегчения восприятия данной модели рассмотрим несколько геометрический примеров.

Пример 1. Дана окружность радиусом 1 см. Чему равна длина окружности, её половины, её четверти?

Решение. Длина L окружности радиусом R вычисляется по формуле L = 2πR, где π≈3,14. Если R = 1 см, то L = 2π см ≈ 6,28 см.

Длина половины окружности равна π см, а длина четверти окружности (AB, BC, CD или DA) равна 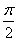см.

Ответ: ≈6,28 см; ≈3,14 см; ≈1,57 см.

Будем говорить об окружности, радиус которой равен масштабному отрезку, без указания конкретных единиц измерения. Радиус такой окружности считается равным 1, а сама окружность наывается единичной. Будем пользоваться единичной окружностью, в которой проведены горизонтальный и вертикальный диаметры CA и DB. Будем называть дугу AB первой четвертью, дугу BC — второй четвертью, дугу CD — третьей четвертью, дугу DA — четвертой четвертью. При этом, как правило, речь идет об открытых дугах, т.е. о дугах без их концов: например, первая четверть — это дуга AB без точек A и B.